Opinión del centro científico Kinesport
Pegatina verde
Pegatina verde
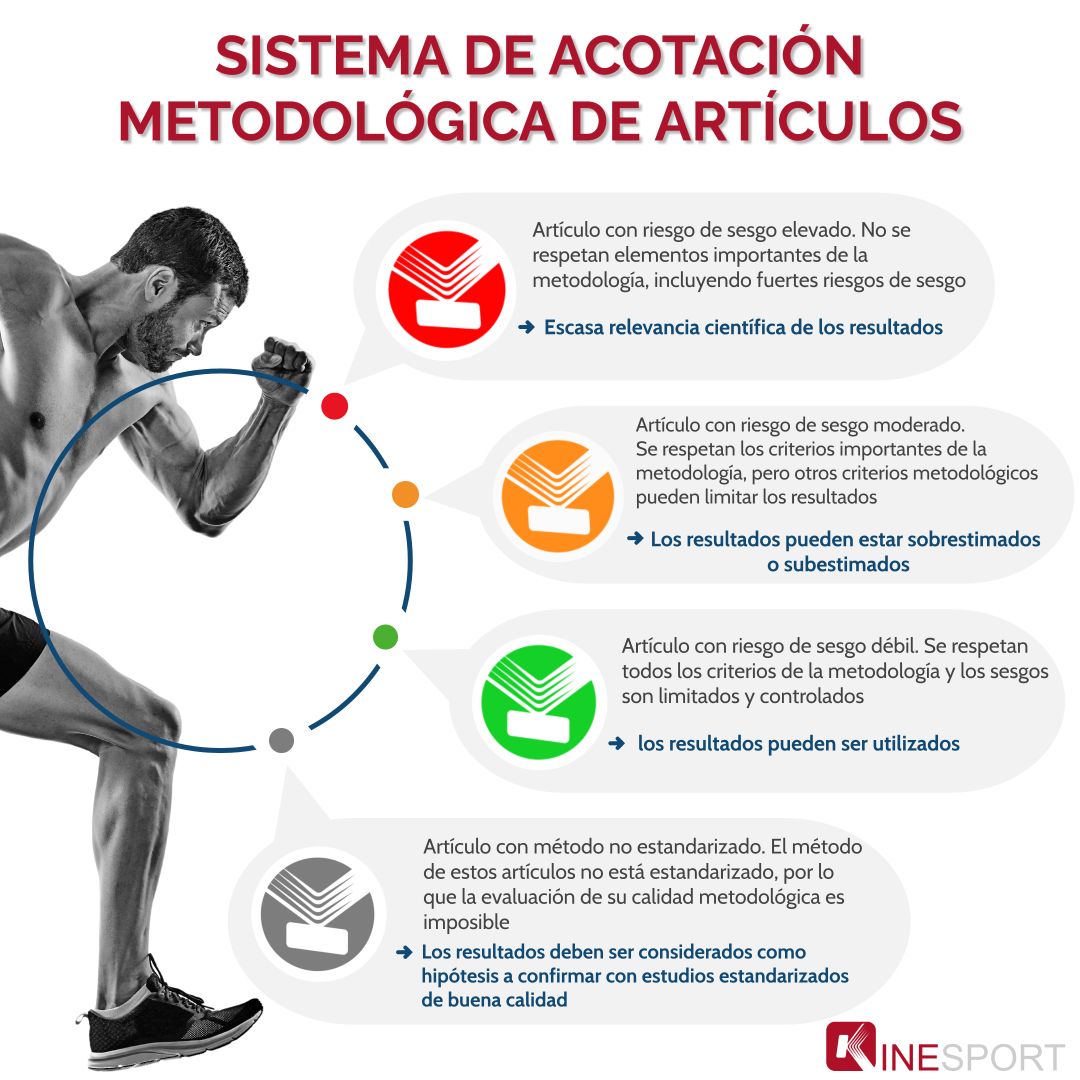
Este estudio longitudinal retrospectivo es un artículo de bajo riesgo de sesgo, en el que se cumplen todos los criterios metodológicos principales para limitar y controlar al máximo el sesgo en el estudio.
Sin embargo, se han notificado varias limitaciones relativas a la estabilidad del modelo, la interpretabilidad de los parámetros, el mal condicionamiento y la precisión predictiva. Estos modelos se consideran modelos lineales variables en el tiempo según la estructura de sus componentes y, por tanto, pueden requerir un número de observaciones (es decir, rendimientos) para estimar correctamente las relaciones entre la carga de entrenamiento y el rendimiento. Para superar algunas de estas limitaciones, se han propuesto mejoras del antiguo modelo de respuesta al impulso utilizando un algoritmo recursivo para estimar los parámetros en función de cada entrada del modelo (es decir, la carga de entrenamiento) e introduciendo variaciones en la respuesta a la fatiga a lo largo de un único ciclo de entrenamiento. También se han desarrollado otras adaptaciones del modelo Fitness-Fatiga con el objetivo de mejorar tanto la bondad del ajuste como la precisión de las predicciones. No obstante, los modelos de respuesta al impulso han tratado de resumir los procesos fisiológicos subyacentes que intervienen en el ejercicio en un número reducido de entidades para predecir los efectos del entrenamiento tanto en actividades de resistencia (carrera, ciclismo, esquí y natación) como en actividades más complejas (lanzamiento de martillo, gimnasia y judo). Este enfoque simplista puede impedir que se capte la relación adecuada entre el entrenamiento y el rendimiento y, en última instancia, dificultar la precisión de las predicciones. Además, con la excepción de Matabuena et al, estos modelos asumen que el efecto del entrenamiento es máximo al final de la sesión de entrenamiento. Esta suposición sólo es razonable para el componente negativo del modelo (es decir, "Fatiga"), cuyo valor máximo se toma inmediatamente después de la sesión. En el caso de los efectos positivos inducidos por el entrenamiento (es decir, la "aptitud"), esta respuesta es bastante cuestionable, ya que las adaptaciones fisiológicas continúan inmediatamente después del final de la sesión de ejercicio. Por ejemplo, se sabe que las adaptaciones del músculo esquelético al entrenamiento, descritas por el aumento de la masa muscular, los índices de acortamiento de las fibras y los cambios en la actividad de la miosina ATPasa, son progresivas y no instantáneas. Por lo tanto, se han propuesto funciones seriales y biexponenciales para contrarrestar estas limitaciones y describir mejor las adaptaciones al entrenamiento mediante funciones exponenciales de crecimiento y decaimiento, basadas en las respuestas fisiológicas de las ratas.
Se utilizó un enfoque más estadístico para investigar los efectos de la carga de entrenamiento en el rendimiento mediante el análisis de componentes principales y modelos lineales mixtos en diferentes periodos de tiempo. Estos modelos infieren los parámetros a partir de todos los datos disponibles (es decir, combinando sujetos en lugar de un modelo por sujeto) pero permiten que los parámetros varíen en función de la heterogeneidad entre los deportistas. Como el modelo es multivariado, la naturaleza multidimensional del rendimiento podría mantenerse incluyendo información psicológica, nutricional y técnica como predictores. Sin embargo, los autores no tuvieron en cuenta la faceta acumulativa de las cargas de entrenamiento diarias, donde las funciones acumulativas exponenciales y decrecientes propuestas por Candau et al. pueden ser adecuadas para modelar el rendimiento.
También se han utilizado alternativas del campo de la informática para aclarar la relación carga de entrenamiento-rendimiento con fines predictivos. En particular, los enfoques de aprendizaje automático se centran generalmente en la generalización del modelo (es decir, la precisión con la que un modelo es capaz de predecir los valores de los resultados para los nuevos datos). Varios enfoques tienden a maximizar dicho criterio. Por ejemplo, pueden realizarse procedimientos de validación cruzada (CV), en los que los datos se separan en conjuntos de entrenamiento para la estimación de parámetros y conjuntos de prueba para la predicción. Este procedimiento favorece la determinación de modelos óptimos, con respecto a la familia de modelos considerada y con respecto a su generalizabilidad. Al mismo tiempo, los procedimientos de CV permiten diagnosticar el infra y el sobreajuste de los modelos. El infraajuste suele describir un modelo inflexible que no es capaz de captar regularidades notables en un conjunto típico de observaciones. Por el contrario, la sobreadaptación representa un modelo sobreentrenado, que tiende a memorizar cada observación particular, lo que conduce a altas tasas de error al predecir sobre datos desconocidos. Mientras que los estudios anteriores pretendían describir la relación entre la carga de entrenamiento y el rendimiento mediante la estimación de los parámetros del modelo y la comprobación del mismo en un único conjunto de datos, no se puede garantizar la generalización de los modelos. Esto pone en duda su utilidad en una aplicación predictiva. Por otra parte, las metodologías de modelización que utilizan procedimientos de CV son la norma con fines de predicción, en lugar de ser únicamente descriptivas. Hasta donde saben los autores, sólo unos pocos estudios recientes han modelado el rendimiento con modelos de fitness-fatiga utilizando un procedimiento de CV, y uno de ellos separó los datos en dos conjuntos iguales de datos de entrenamiento y de prueba respectivamente. Ludwig et al. informaron de que la optimización de todos los parámetros, incluido el término de retardo, hace que el modelo sea propenso al sobreajuste. Como resultado, las interpretaciones de las predicciones, así como los parámetros del modelo, pueden ser incorrectos.
Dado que las adaptaciones fisiológicas implicadas en el ejercicio son complejas, algunos autores han estudiado la relación entre el entrenamiento y el rendimiento utilizando redes neuronales artificiales (RNA), modelos de aprendizaje automático no lineal. A pesar de los pequeños errores de predicción notificados (por ejemplo, un error de 0,05 segundos en un rendimiento de 200 metros de natación), las consideraciones metodológicas de su estudio (influidas principalmente por un tamaño de muestra pequeño) y la naturaleza de caja negra de las RNA, ponen en duda su uso en la modelización del rendimiento deportivo. La informática ofrece muchos modelos de aprendizaje automático, aunque a menudo se reducen en las RNA a la predicción del rendimiento deportivo. Al considerar el rendimiento deportivo, también podrían considerarse potentes algoritmos del aprendizaje supervisado para resolver los problemas de modelización del rendimiento deportivo, ya sea mediante la regresión o mediante una formulación de clasificación del problema. Por nombrar algunos, los enfoques no lineales, como los modelos Random Forest (RF), tienen en cuenta las relaciones no lineales entre un objetivo y un gran conjunto de predictores para hacer predicciones. De manera diferente, los modelos lineales, como las regresiones lineales regularizadas, también han demostrado ser eficaces en contextos de alta dimensionalidad y multicolinealidad. Sobre esta base, ambos podrían ser útiles para la modelización del rendimiento deportivo.
Hasta la fecha, ninguna familia de modelos (es decir, modelos de respuesta al impulso, basados en la fisiología, estadísticos y de aprendizaje automático) parece estar favorecida para predecir el rendimiento deportivo a partir de un conjunto de datos, principalmente debido a la falta de pruebas y de confianza en la modelización de los efectos del entrenamiento y la precisión de las predicciones de rendimiento. Además, al no evaluarse sistemáticamente la generalizabilidad, las interpretaciones prácticas y fisiológicas de algunos modelos pueden ser incorrectas y deben tomarse con precaución.
Con el fin de dilucidar la relación entre las cargas de entrenamiento y el rendimiento deportivo en una aplicación predictiva, los autores plantearon la hipótesis de que, tras la selección del modelo, los métodos de regularización y reducción de la dimensión conducirían a una mayor capacidad de generalización del modelo que los antiguos modelos de respuesta al impulso.
Para prescribir programas de entrenamiento óptimos, los profesionales del deporte deben comprender los efectos fisiológicos que conlleva cada sesión de entrenamiento y sus consecuencias en el rendimiento deportivo. Así pues, este estudio pretendía proporcionar una metodología robusta y transferible basada en la generalización de modelos en un contexto de modelización del rendimiento deportivo. Los autores recogieron datos de patinadores de velocidad de pista corta de alto nivel que eran miembros del equipo nacional francés. Hasta la fecha, sólo unos pocos estudios han investigado la relación entre el entrenamiento y el rendimiento en este deporte. Utilizando enfoques de modelización lineal y no lineal, Knobbe et al. proporcionaron una interesante metodología en torno a los métodos de agregación para proporcionar características clave y procesables de los componentes de formación. Los autores investigaron los modelos individuales que representan las adaptaciones al entrenamiento y que podrían proporcionar información útil a los entrenadores que participan en las tareas de programación del entrenamiento. Por otra parte, Méline et al. examinaron la relación dosis-respuesta entre el entrenamiento y el rendimiento mediante simulaciones de sobrecarga y algunas estrategias de reducción progresiva. El modelo de dosis-respuesta de Busso surgió como un modelo valioso para evaluar las estrategias de reducción y sus efectos potenciales en el rendimiento del patinaje. Sin embargo, una contribución basada principalmente en el principio de generalización del modelo parece interesante para mejorar el conocimiento de la modelización del rendimiento deportivo en los deportes de alto rendimiento.
Tras construir un conjunto de datos adecuado, los autores consideraron el modelo dosis-respuesta (DR) como un esquema básico de regresión y lo compararon con tres modelos: la regresión de componentes principales (PCR), la regresión de red elástica (ENET) y la regresión de bosque aleatorio (RF). Estos modelos nos permiten :
- Presentar y discutir la utilidad de los métodos de regularización y reducción de dimensión en relación con el concepto de generalización.
- Modelar el rendimiento deportivo mediante modelos robustos de alta dimensión y multilinealidad y estudiar los factores clave del rendimiento en el patinaje de velocidad en pista corta.
Métodos
Se trata de un estudio longitudinal retrospectivo
Participantes
-
Edad media 22,7 ± 3,4 años
-
3 hombres (masa corporal de 71,4 ± 9,4 kg)
-
4 mujeres (masa corporal de 55,9 ± 3,9 kg)
Cada atleta experimentó los Juegos Olímpicos de Invierno de 2018 en PyeongChang, Corea del Sur (n=2) o se estaba preparando para los Juegos Olímpicos de Pekín, China (n=7).
Todo el equipo fue dirigido por el mismo entrenador, que se encargó de programar las sesiones de entrenamiento y de recoger los datos. El volumen medio de entrenamiento semanal fue de 16,6 ± 2,5 horas.
Los datos se recogieron durante un periodo de entrenamiento de tres meses sin competición, interrumpido por un descanso de dos semanas y que comenzó un mes después de reanudar el entrenamiento para una nueva temporada.
El presente estudio retrospectivo utilizó los datos recogidos sin provocar ningún cambio en el programa de entrenamiento de los atletas.
Conjunto de datos
Variable dependiente: rendimiento
Los participantes realizaron semanalmente pruebas contrarreloj de pie (distancia = 166,68 metros, o 1,5 vueltas) tras un calentamiento estandarizado.
Se registraron 248 actuaciones para una media de 35,4±2,23 actuaciones individuales.
Como la prueba de rendimiento es un estándar de oro para la evaluación de la capacidad de aceleración, todos los atletas estaban familiarizados con esta prueba antes del estudio.
Resumen de las variables independientes
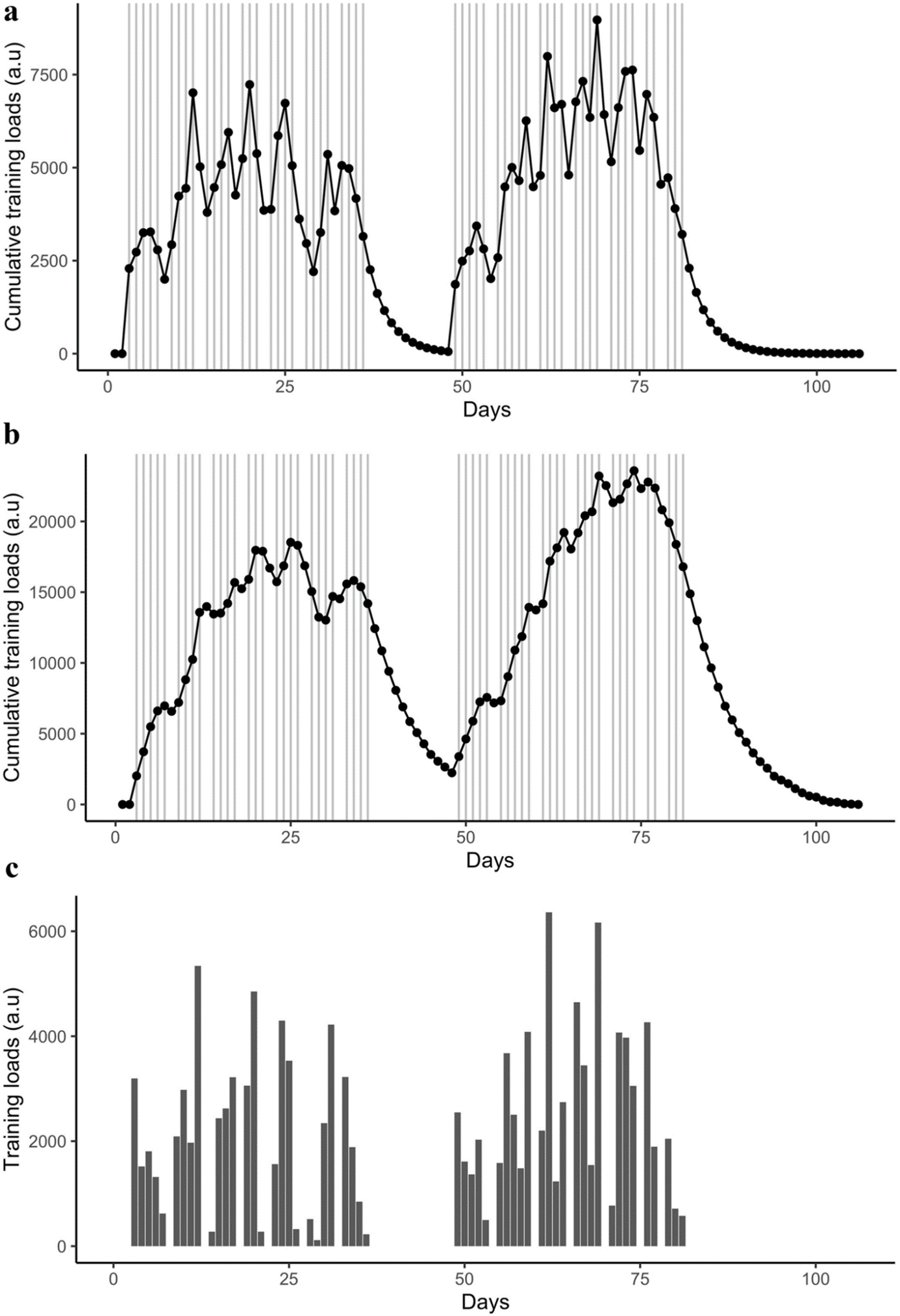
Cargas de entrenamiento diarias acumuladas de un atleta representativo siguiendo (a) la función de respuesta al impulso y la función de respuesta biexponencial en serie. (c) muestra las cargas de entrenamiento diarias brutas X1 , expresadas como w(t). En (a) y (b), los puntos representan los valores diarios de la carga de entrenamiento acumulada y las líneas verticales sólidas indican la ocurrencia de las sesiones de entrenamiento. Los valores se representan en unidades arbitrarias (a.u).
Resultados
Mediante la validación cruzada de las series temporales, los modelos proporcionaron una generalización y una predicción del rendimiento heterogéneas. Aquí se muestran las distribuciones de los errores cuadráticos medios por modelo:
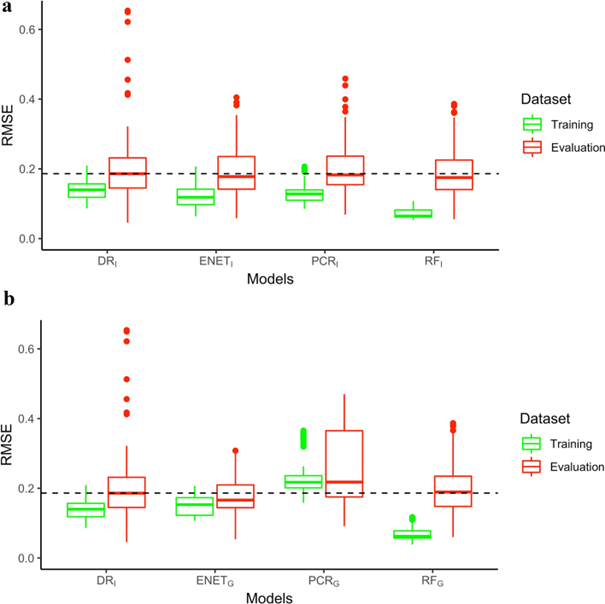
Generalización de los modelos
El análisis de modelos mixtos mostró que los modelos ENET y PCR redujeron las diferencias en los errores de predicción entre los conjuntos de datos de entrenamiento y de evaluación.
Los modelos más generalizables fueron los modelos ENET y PCR calculados sobre datos agregados, seguidos de los modelos basados en individuos. En general, es probable que los modelos basados en grupos sean más generalizables que los modelos basados en individuos.
Predicción de rendimiento
Los errores cuadráticos medios (RMSE) registrados en los datos de evaluación mediante un análisis de modelos mixtos indicaron que ENETG fue el modelo que más contribuyó a reducir los errores de predicción, seguido de RFG . Por lo tanto, se ha constatado un efecto significativo de la clase de modelo sobre los errores de predicción. El cálculo de los modelos en una población más grande (es decir, los modelos basados en grupos) sólo mostró una tendencia a favor de los modelos basados en grupos en la tasa de respuesta de error.
Las distribuciones del RMSE en los datos utilizados para la evaluación del modelo mostraron una varianza heterogénea entre los modelos. Las mayores desviaciones estándar se encontraron en el caso de DRI y PCRG . Los modelos ENET, PCRI y RF tuvieron un rendimiento más consistente con desviaciones estándar más bajas en los rangos [0,023; 0,027] y [0,012; 0,017] para los modelos calculados individualmente y en grupo, respectivamente.
Las predicciones realizadas a partir de los dos modelos más generalizables (ENETG y PCRG ), y la referencia DRI ilustran la sensibilidad de los modelos para un atleta representativo:
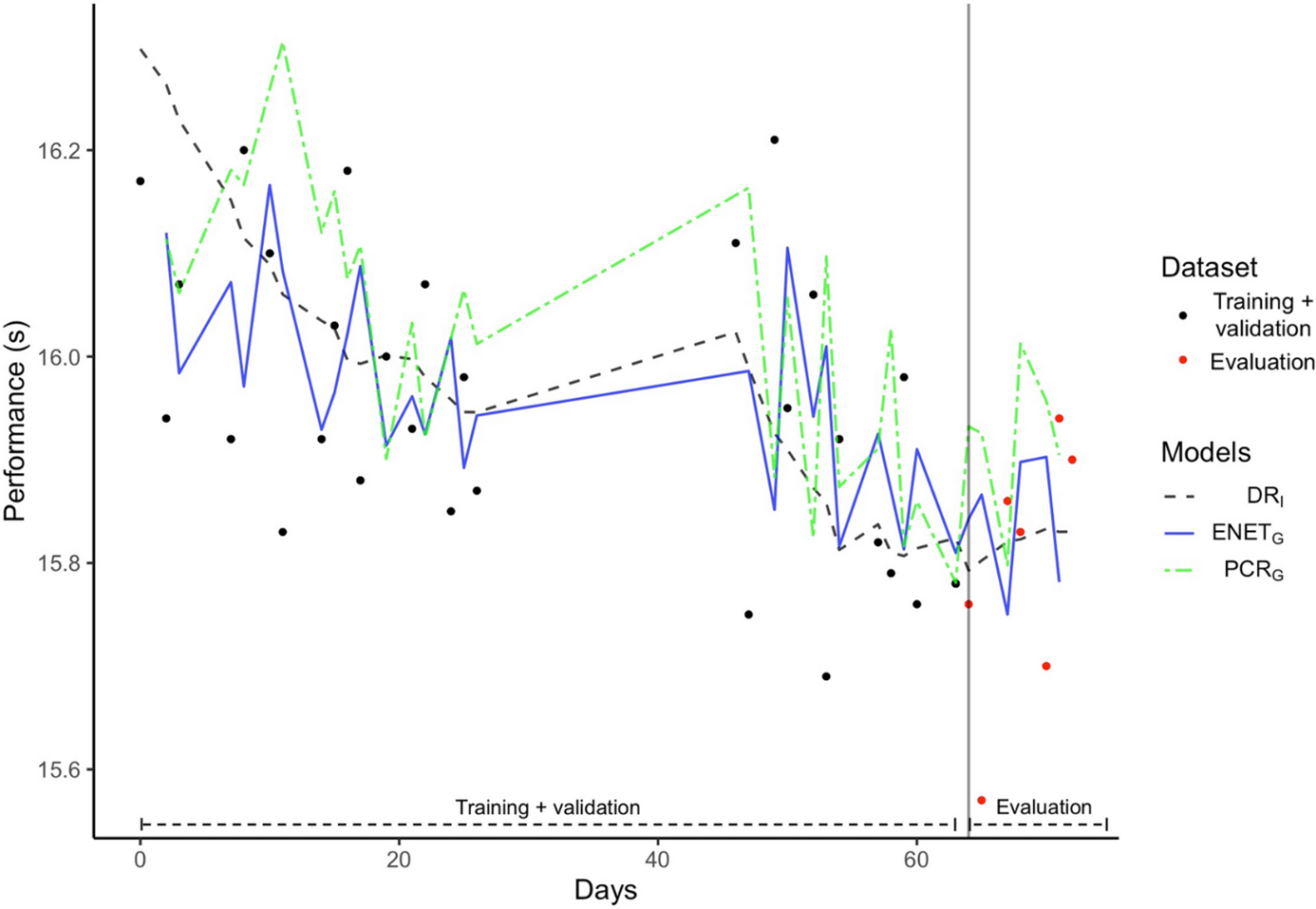
El rendimiento modelado a partir del modelo DRI era relativamente estable y menos sensible a las variaciones de rendimiento reales. La desviación estándar calculada sobre los datos utilizados para la evaluación del modelo confirma esta predicción consistente con σ=0,015, σ=0,071 y σ=0,062 para DRi , PCRG y ENETG , respectivamente. En el caso de ENETG , los coeficientes estandarizados más elevados se atribuyeron al componente autorregresivo (es decir, los resultados anteriores), seguido del factor atleta y, a continuación, de los agregados impulsivos y biexponenciales en serie. Para la regresión, la RCPG utilizó los tres primeros componentes principales que explican el 52,3%, el 16,5% y el 7,6% de la varianza total, respectivamente.
Conclusión
- Este estudio nos proporciona una metodología de modelización transferible basada en la evaluación de la generalizabilidad de los modelos en un contexto de modelización del rendimiento deportivo.
- El modelo matemático dosis-respuesta con la Red Elástica (ENET), la Regresión de Componentes Principales (PCR) y los modelos de Bosque Aleatorio (RF) fueron validados de forma cruzada en un marco de series temporales.
- La generalización del modelo DR (dosis-respuesta) fue superada por los modelos ENET y PCR, aunque los resultados no pueden compararse directamente con la literatura.
- El modelo ENET proporcionó el mejor rendimiento tanto en términos de generalización como de precisión en la predicción del rendimiento en comparación con los modelos DR, PCR y RF.
- En general, el aumento del tamaño de la muestra mediante el cálculo de modelos en todo el grupo de atletas dio lugar a modelos de mejor rendimiento que los calculados individualmente.
- En este estudio, se favoreció el uso de métodos de regularización y reducción de la dimensión para tratar los problemas de alta dimensionalidad y multicolinealidad. Sin embargo, otros modelos podrían ser útiles para modelar el rendimiento deportivo.
- La metodología destacada en este estudio puede reutilizarse independientemente de los datos, con el objetivo de optimizar el rendimiento en el deporte de élite mediante protocolos de entrenamiento simulados.
- Otras investigaciones que incluyan simulaciones de sesiones de entrenamiento y evaluaciones de modelos en el ámbito de la previsión pondrían de manifiesto la pertinencia de determinadas familias de modelos para la optimización de la programación del entrenamiento.
Referencia del artículo
Imbach F, Perrey S, Chailan R, Meline T, Candau R. Modelización de respuestas a la carga de entrenamiento y generalización de modelos en deportes de élite. Sci Rep. 2022 Jan 28;12(1):1586. doi: 10.1038/s41598-022-05392-8. PMID: 35091649; PMCID: PMC8799698.